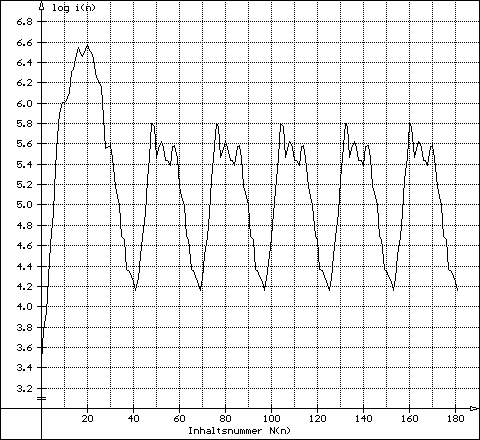
Aliquot Sequence Program
Betrothed numbers or quasi-amicable numbers are two positive integers such that the sum of the proper divisors of either number is one more than the value of the other number. In other words, (m, n) are a pair of betrothed numbers if s(m) = n + 1 and s(n) = m + 1, where s(n) is the aliquot sum of n: an equivalent condition is that σ(m) = σ(n) = m + n + 1, where σ denotes the sum-of. Definition and overview. The aliquot sequence starting with a positive integer k can be defined formally in terms of the sum-of-divisors function σ 1 or the aliquot sum function s in the following way. S 0 = k s n = s(s n−1) = σ 1 (s n−1) − s n−1 if s n−1 0 s n = 0 if s n−1 = 0 - (if we add this condition, then the terms after 0 are all 0, and all Aliquot sequences would be.
| Unsolved problem in mathematics: Do all aliquot sequences eventually end with a prime number, a perfect number, or a set of amicable or sociable numbers? (Catalan's aliquot sequence conjecture) (more unsolved problems in mathematics) |
In mathematics, an aliquot sequence is a sequence of positive integers in which each term is the sum of the proper divisors of the previous term. If the sequence reaches the number 1, it ends, since the sum of the proper divisors of 1 is 0.
Definition and overview[edit]
The aliquot sequence starting with a positive integer k can be defined formally in terms of the sum-of-divisors function σ1 or the aliquot sum function s in the following way:[1]
Godrej Properties Platinum. 45 Years of Experience. Ongoing Projects. Projects by Puravankara. Puravankara Purva Atmosphere. Puravankara Skywood. Provident Housing. 45 Years of Experience. Ongoing Projects. Projects by Provident Housing. Provident Housing Capella 1. Provident Housing Welworth City. 23 Years of Experience. Ongoing Projects. Builders list in bangalore pdf. LIST OF APPROVED BUILDERS NEW LIST FROM 01.09. KEY PERSON NAME &MOBILE NUMBER. 1 MUMBAI AHMEDABAD M/s. ARMAAN DEVELOPERS, B-404, Commercial House-5, Opp. Vodafone Building, Prahaladnagar, Ahmedabad 1 Mr. Sunit Bhai S. Chowksi, Mob. SYNB-ZOM-AHM-0001 2 MUMBAI AHMEDABAD M/s.
- s0 = k
- sn = s(sn−1) = σ1(sn−1) − sn−1 if sn−1 > 0
- sn = 0 if sn−1 = 0 ---> (if we add this condition, then the terms after 0 are all 0, and all Aliquot sequences would be infinite sequence, and we can conjecture that all Aliquot sequences are convergent, the limit of these sequences are usually 0 or 6)
and s(0) is undefined.
For example, the aliquot sequence of 10 is 10, 8, 7, 1, 0 because:
- σ1(10) − 10 = 5 + 2 + 1 = 8,
- σ1(8) − 8 = 4 + 2 + 1 = 7,
- σ1(7) − 7 = 1,
- σ1(1) − 1 = 0.
Many aliquot sequences terminate at zero; all such sequences necessarily end with a prime number followed by 1 (since the only proper divisor of a prime is 1), followed by 0 (since 1 has no proper divisors). See (sequence A080907 in the OEIS) for a list of such numbers up to 75. There are a variety of ways in which an aliquot sequence might not terminate:
- A perfect number has a repeating aliquot sequence of period 1. The aliquot sequence of 6, for example, is 6, 6, 6, 6, ..
- An amicable number has a repeating aliquot sequence of period 2. For instance, the aliquot sequence of 220 is 220, 284, 220, 284, ..
- A sociable number has a repeating aliquot sequence of period 3 or greater. (Sometimes the term sociable number is used to encompass amicable numbers as well.) For instance, the aliquot sequence of 1264460 is 1264460, 1547860, 1727636, 1305184, 1264460, ..
- Some numbers have an aliquot sequence which is eventually periodic, but the number itself is not perfect, amicable, or sociable. For instance, the aliquot sequence of 95 is 95, 25, 6, 6, 6, 6, .. . Numbers like 95 that are not perfect, but have an eventually repeating aliquot sequence of period 1 are called aspiring numbers.[2]
| n | Aliquot sequence of n | length (OEIS: A098007) | n | Aliquot sequence of n | length (OEIS: A098007) | n | Aliquot sequence of n | length (OEIS: A098007) | n | Aliquot sequence of n | length (OEIS: A098007) |
| 0 | 0 | 1 | 12 | 12, 16, 15, 9, 4, 3, 1, 0 | 8 | 24 | 24, 36, 55, 17, 1, 0 | 6 | 36 | 36, 55, 17, 1, 0 | 5 |
| 1 | 1, 0 | 2 | 13 | 13, 1, 0 | 3 | 25 | 25, 6 | 2 | 37 | 37, 1, 0 | 3 |
| 2 | 2, 1, 0 | 3 | 14 | 14, 10, 8, 7, 1, 0 | 6 | 26 | 26, 16, 15, 9, 4, 3, 1, 0 | 8 | 38 | 38, 22, 14, 10, 8, 7, 1, 0 | 8 |
| 3 | 3, 1, 0 | 3 | 15 | 15, 9, 4, 3, 1, 0 | 6 | 27 | 27, 13, 1, 0 | 4 | 39 | 39, 17, 1, 0 | 4 |
| 4 | 4, 3, 1, 0 | 4 | 16 | 16, 15, 9, 4, 3, 1, 0 | 7 | 28 | 28 | 1 | 40 | 40, 50, 43, 1, 0 | 5 |
| 5 | 5, 1, 0 | 3 | 17 | 17, 1, 0 | 3 | 29 | 29, 1, 0 | 3 | 41 | 41, 1, 0 | 3 |
| 6 | 6 | 1 | 18 | 18, 21, 11, 1, 0 | 5 | 30 | 30, 42, 54, 66, 78, 90, 144, 259, 45, 33, 15, 9, 4, 3, 1, 0 | 16 | 42 | 42, 54, 66, 78, 90, 144, 259, 45, 33, 15, 9, 4, 3, 1, 0 | 15 |
| 7 | 7, 1, 0 | 3 | 19 | 19, 1, 0 | 3 | 31 | 31, 1, 0 | 3 | 43 | 43, 1, 0 | 3 |
| 8 | 8, 7, 1, 0 | 4 | 20 | 20, 22, 14, 10, 8, 7, 1, 0 | 8 | 32 | 32, 31, 1, 0 | 4 | 44 | 44, 40, 50, 43, 1, 0 | 6 |
| 9 | 9, 4, 3, 1, 0 | 5 | 21 | 21, 11, 1, 0 | 4 | 33 | 33, 15, 9, 4, 3, 1, 0 | 7 | 45 | 45, 33, 15, 9, 4, 3, 1, 0 | 8 |
| 10 | 10, 8, 7, 1, 0 | 5 | 22 | 22, 14, 10, 8, 7, 1, 0 | 7 | 34 | 34, 20, 22, 14, 10, 8, 7, 1, 0 | 9 | 46 | 46, 26, 16, 15, 9, 4, 3, 1, 0 | 9 |
| 11 | 11, 1, 0 | 3 | 23 | 23, 1, 0 | 3 | 35 | 35, 13, 1, 0 | 4 | 47 | 47, 1, 0 | 3 |
The lengths of the Aliquot sequences that start at n are
- 1, 2, 2, 3, 2, 1, 2, 3, 4, 4, 2, 7, 2, 5, 5, 6, 2, 4, 2, 7, 3, 6, 2, 5, 1, 7, 3, 1, 2, 15, 2, 3, 6, 8, 3, 4, 2, 7, 3, 4, 2, 14, 2, 5, 7, 8, 2, 6, 4, 3, .. (sequence A044050 in the OEIS)
The final terms (excluding 1) of the Aliquot sequences that start at n are
- 1, 2, 3, 3, 5, 6, 7, 7, 3, 7, 11, 3, 13, 7, 3, 3, 17, 11, 19, 7, 11, 7, 23, 17, 6, 3, 13, 28, 29, 3, 31, 31, 3, 7, 13, 17, 37, 7, 17, 43, 41, 3, 43, 43, 3, 3, 47, 41, 7, 43, .. (sequence A115350 in the OEIS)
Numbers whose Aliquot sequence terminates in 1 are
Gui exiftool for mac. You can edit any tag that is displayed. Batch editingExifTool supports batch exif deletion and editing too, all you have to is add several images after the command. Want to add tags? Here is a, and one more which mentions all in Windows.
- 1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 26, 27, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, .. (sequence A080907 in the OEIS)
Numbers whose Aliquot sequence known to terminate in a perfect number, other than perfect numbers themselves (6, 28, 496, ..), are
- 25, 95, 119, 143, 417, 445, 565, 608, 650, 652, 675, 685, 783, 790, 909, 913, .. (sequence A063769 in the OEIS)
Numbers whose Aliquot sequence terminates in a cycle with length at least 2 are
- 220, 284, 562, 1064, 1184, 1188, 1210, 1308, 1336, 1380, 1420, 1490, 1604, 1690, 1692, 1772, 1816, 1898, 2008, 2122, 2152, 2172, 2362, .. (sequence A121507 in the OEIS)
Numbers whose Aliquot sequence is not known to be finite or eventually periodic are
- 276, 306, 396, 552, 564, 660, 696, 780, 828, 888, 966, 996, 1074, 1086, 1098, 1104, 1134, 1218, 1302, 1314, 1320, 1338, 1350, 1356, 1392, 1398, 1410, 1464, 1476, 1488, .. (sequence A131884 in the OEIS)
A number that is never the successor in an aliquot sequence is called an untouchable number.
- 2, 5, 52, 88, 96, 120, 124, 146, 162, 188, 206, 210, 216, 238, 246, 248, 262, 268, 276, 288, 290, 292, 304, 306, 322, 324, 326, 336, 342, 372, 406, 408, 426, 430, 448, 472, 474, 498, .. (sequence A005114 in the OEIS)
Catalan-Dickson conjecture[edit]
An important conjecture due to Catalan, sometimes called the Catalan–Dickson conjecture, is that every aliquot sequence ends in one of the above ways: with a prime number, a perfect number, or a set of amicable or sociable numbers.[3] The alternative would be that a number exists whose aliquot sequence is infinite yet never repeats. Any one of the many numbers whose aliquot sequences have not been fully determined might be such a number. The first five candidate numbers are often called the Lehmer five (named after D.H. Lehmer): 276, 552, 564, 660, and 966.[4] However, it is worth noting that 276 may reach a high apex in its aliquot sequence and then descend; the number 138 reaches a peak of 179931895322 before returning to 1.
Guy and Selfridge believe the Catalan–Dickson conjecture is false (so they conjecture some aliquot sequences are unbounded above (or diverge)).[5]
As of April 2015, there were 898 positive integers less than 100,000 whose aliquot sequences have not been fully determined, and 9190 such integers less than 1,000,000.[6]
Systematically searching for aliquot sequences[edit]
The aliquot sequence can be represented as a directed graph, , for a given integer , where denotes thesum of the proper divisors of .[7]Cycles in represent sociable numbers within the interval . Two special cases are loops that represent perfect numbers and cycles of length two that represent amicable pairs.
See also[edit]
Notes[edit]
- ^Weisstein, Eric W.'Aliquot Sequence'. MathWorld.
- ^Sloane, N. J. A. (ed.). 'Sequence A063769 (Aspiring numbers: numbers whose aliquot sequence terminates in a perfect number.)'. The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^Weisstein, Eric W.'Catalan's Aliquot Sequence Conjecture'. MathWorld.
- ^Creyaufmüller, Wolfgang (May 24, 2014). 'Lehmer Five'. Retrieved June 14, 2015.
- ^A. S. Mosunov, What do we know about aliquot sequences?
- ^Creyaufmüller, Wolfgang (April 29, 2015). 'Aliquot Pages'. Retrieved June 14, 2015.
- ^Rocha, Rodrigo Caetano; Thatte, Bhalchandra (2015), Distributed cycle detection in large-scale sparse graphs, Simpósio Brasileiro de Pesquisa Operacional (SBPO), doi:10.13140/RG.2.1.1233.8640
References[edit]

- Manuel Benito; Wolfgang Creyaufmüller; Juan Luis Varona; Paul Zimmermann. Aliquot Sequence 3630 Ends After Reaching 100 Digits. Experimental Mathematics, vol. 11, num. 2, Natick, MA, 2002, p. 201-206.
- W. Creyaufmüller. Primzahlfamilien - Das Catalan'sche Problem und die Familien der Primzahlen im Bereich 1 bis 3000 im Detail. Stuttgart 2000 (3rd ed.), 327p.
External links[edit]
- Tables of Aliquot Cycles (J.O.M. Pedersen)
- Aliquot Page (Wolfgang Creyaufmüller)
- Aliquot sequences (Christophe Clavier)
- Forum on calculating aliquot sequences (MersenneForum)
- Aliquot sequence summary page for sequences up to 100000 (there are similar pages for higher ranges) (Karsten Bonath)
- Active research site on aliquot sequences (Jean-Luc Garambois) (in French)
In, a sublime number is a positive which has a of positive (including itself), and whose positive factors add up to another perfect number.The number, for example, is a sublime number. It has a perfect number of positive factors : 1, 2, 3, 4, 6, and 12, and the sum of these is again a perfect number: 1 + 2 + 3 + 4 + 6 + 12 =.There are only two known sublime numbers, 12 and (2 126)(2 61 − 1)(2 31 − 1)(2 19 − 1)(2 7 − 1)(2 5 − 1)(2 3 − 1) (sequence in the ). The second of these has 76 decimal digits:691264.
References.